Industrial sectors’ investment levels k_IK and household sectors’ savings levels g_LK have been described in terms of absorbing the sectors’ respective net cash flows -r_IK. These presentations will now be connected by linking industries’ generation of dividends -e_IK to households’ receipt of dividends e_LK.

Model 0 is limited to a single financial intermediary per economy K. One interest rate -i_K controls all of K’s capital investment positions k_IK, and one investment term T_K controls all of K’s savings positions -g_LK. K’s intermediary is presumed to maintain contra-accounts k_0K and g_0K opposite these financial positions:

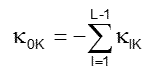
It will be noted that 1) k_0K is a negative quantity; 2) g_0K is a positive quantity; and 3) nothing requires that these quanta offset one another. Leverage, -k_0K/g_0K>1, is (as will be shown) the norm in capitalist systems: it is a requisite of capital development, and it persists in a stable equilibrium.

The interest rate -i_K controlling capital positions k_IK, and the investment term T_K controlling saving positions -g_LK, are brought together in the familiar notion of net present value NPV:

This transcendental expression of net present value is incomplete from the standpoint of our analysis because it carries no awareness of economy K’s leverage, which is expressed in the intermediary’s unequal investment k_0K and savings g_0K contra-accounts. (Subscripts K and 0 are hereafter eliminated for notational convenience on the understanding that unsubscripted variables belong to the single intermediary allowed to a given economy.)

These considerations are brought out in an algebraic expression of net present value in terms of the intermediary’s contra-accounts k and g:

Having narrowed our view to a single intermediary managing a portfolio composed of all an economy K's productive assets a_K, we have conjured circumstances in which all returns on investment i·k accrue to savings of g that are committed for T years. The algebraic expression for NPV shows a cash flow of g/T+i·k for delivery in T years that is being continually purchased for a cash flow of g/T that is being tendered now. Risk is introduced to the model insofar as i and T are variables, and the value of the currency in which savings g are denominated is also subject to change during the investment term.

This equation can be transformed as follows so as to isolate the interest rate, investment term, and leverage:

Noting that 1) k and g are state variables, and 2) the interest rate -i was determined earlier, it is obvious that NPV can be eliminated from the simultaneous system composed by its transcendental and algebraic expressions above. This leaves us with one equation in which the only unknown is the investment term T. While closed-form calculations for T are not possible with this system, its practical application can be achieved through a Newton-Raphson approximation to its simultaneous solution.

With T and NPV known, we turn to the computations by which the industrial sectors’ dividends e_IK=i_K·k_IK are distributed among the household sectors in proportion to their savings positions -g_LK. Solving the algebraic NPV equation for the intermediary’s harvest of returns i·k yields the return to his savings contra-account g:

Obviously total returns i·k can be scaled by substituting a particular household sector LK’s portion g_LK of total savings -g for this equation’s g in order to compute a specific labor/leisure sector LK’s dividend e_LK. Here it will be convenient to introduce a variable n_K with which to express the annual return on savings expressed in the bracketed term above:

This gives a compact expression for the annual dividends accruing to a given household sector LK:

Model 0’s primitive expression of financial intermediation has an economy K’s single intermediary continuously reckoning K’s interest rate -i_K in order to set K’s investment term T_K so as to completely nullify the net returns on his contra-accounts: