Global demand for a commodity J having
been having been established in terms of constant value units, GCUs per unit of J, we can envision
the determination of absolute global commodity values YJ G/unit through some market
regime based on a global demand function. Given our intention that Model 0 represent a direct
realization of neoclassicism, we naturally choose a perfect market as the appropriate regime.
Global output YJ0 and quanta on the market OJ0 are simply sums on the YJK’s and OJK’s over all K=1…M. (In the case of YJ0 we note that this summation constitutes a further presumption that a sector I’s global production function can be legitimately constructed by merely adding together the corresponding utility parameters for the sectors IK. Again, our justification for this procedure continues the earlier discussion regarding the peculiar nature of hyperbolic indifference surfaces.)
As discussed in connection with global supply and demand, Model 0’s context provides for determinants of global supply SJ0 in terms of current global output rates YJ0 and global market pressure VJ•OJ0:
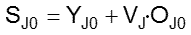
Invoking Say’s assertion that a good J’s supply SJ0 will create
its own demand DJ0, we need only substitute SJ0 for DJ0 in the
global demand schedule in order to compute J’s value YJ G/unit:

Ultimately Model 0’s computations of commodity values operationalize the most pedestrian things to be said about price determination in a free market:
What does the market for commodity J ‘know’ when it sets a price YJ? certainly it has knowledge of the current supply rate SJ to be liquidated.
What information do the sectors I using good J bring to the market? certainly it must be a sense of J’s current marginal value to I, i.e.: the quantity likely to be demanded at each point in a reasonable array of market valuations.
The relationship between the demands of all sectors I for a commodity J and J’s price has long been comprehended in terms of demand schedules.
To the extent that J’s demand schedule can be accurately and continuously re-estimated prior to knowledge of J’s price, the market-clearing price can be computed by substituting the current supply rate SJ for the demand variable.
Finally, we note that the market for any good J functions on the basis of information having no relevance to any other market. Thus markets cannot conspire to formulate a set of prices that will guide an economic system toward general optimality because they each operate on local data that is not known to other markets — and which those markets would not, in any case, have the ability to process.