Our discussion of commodity markets centered on the level O_JK of a commodity J that has been produced in economy K, but remains un-purchased. This quantity is modeled as wasting its economic potential at a rate V_J•O_JK, where V_J is J’s turnover fraction. Model 0's notion of supply S_JK is defined by adding this ‘market pressure’ to the rate Y_JK at which J is currently produced in K:

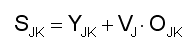
Our discussion of how adjustments to physical asset levels can be controlled identified an individual sector IK’s demand for commodity J Q_IJK as:

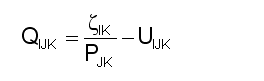
Model 0's notion of domestic demand D_JK sums demands of the sectors I for J in K:

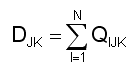
Simple addition across all M of the economies K provides global (K = 0) totals Y_J0, O_J0, S_J0, and D_J0 for all the variables subscripted JK in these equations. Where S_J0 and D_J0 are equal for given commodity J, we can be assured that there exists an export/import profile X_JK such that X_J0 is null, and that all domestic demands D_JK are satisfied by the sum of domestic supply S_JK minus exports X_JK:

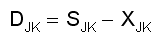
(Per the SFEcon sign convention, a negative value for X_JK indicates a quantity that is imported.)

Working as we are within the neoclassical paradigm, we can anticipate creating a regime of prices that tends to equate demand with supply; but this tendency is necessarily imperfect for any dynamic model — as, indeed, it must be for any objective counterpart of what the model portrays. It is therefore essential to exhibit at least one mechanism whereby the X_JK’s are calculated such that X_J0 will a) approximate zero to the extent that the integer zero can be expressed as a real number by a digital computer, and b) vary from zero in a way that is temporally unbiased to the positive or negative.

This is most easily done by envisioning a quantity D_J’ for the amount of global demand D_J0 that will be satisfied at any given point in time, and a quantity S_J’ for the amount of global supply S_J0 that will be used at any given point in time. At any moment, one of two things must be happening: S_J0 will be diminished to S_J’; or D_J0 will be diminished to D_J’. The factors accomplishing these diminutions are named FS_J and FD_J; and, at any given moment, one of these factors must unity, while the other must be less than unity.

The factors FS_J and FD_J both derive from the ratio F_J of global supply S_J0 to global demand D_J0:

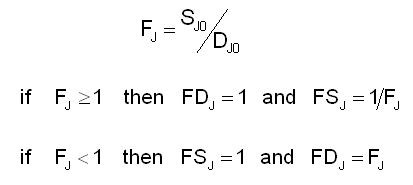
FS_J and FD_J will then determine exports/imports X_JK of commodity J from/to economy K:

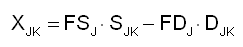
This equation assures the export/import profiles are such that any X_J0 will always compute as close to integer zero as is possible for digital representations of real numbers; and the overall global system never attempts to export more than is imported, or to import more than is exported, irrespective of imbalances between supply and demand.

FD_J also serves to prevent the sectors IK from taking J off the market in excess of what is being supplied:

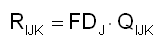
Here we arrive at the final definition of the asset replenishment rate R_IJK that controls SFEcon’s circuit of physical flows. Whenever the global supply of J equals or exceeds global demand and FD_J is unity, the rate R_IJK at which a sector IK takes a commodity J off the market equates to the optimal rate Q_IJK for IK to use J. When supplies of J are not adequate to meet demand, FD_J less-than-unity serves to ration asset replenishment rates. An overabundance of supply for J will be absorbed into the market, where (as we shall see) it depresses prices.

Small negative quanta appearing here and there on the market are allowed as indicia to the model that a given commodity J must be rationed. ‘Conservation of mass’ is required insofar as a market is only allowed to go negative to the extent possible during one differential element of time, given that the market variable began that differential element of time as a positive quantity. Conservation of mass is reinstated by the definition of supply S_JK as output Y_JK plus market pressure V_J•O_JK: where market pressure is a tad negative, supply becomes a tad less than current output; and demands are never allowed to be satisfied in excess of available supply.