Higher-ordered delays are constructed by arranging first-order delays in series such that the effluent of one level cascades into the next. This arrangement is shown below for a third-order delay in which three levels A, B, and C are used to filter and smooth an exogenous input rate R.
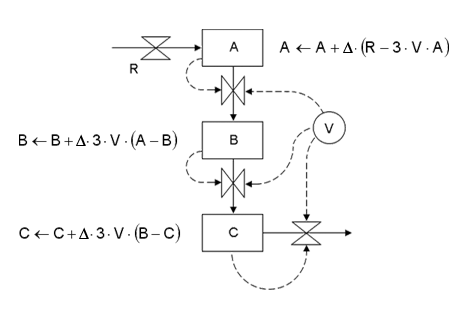
Here the delay on R would be given by E = V•(A + B + C), and equations for continuously re-computing the levels would follow the pattern shown in the diagram. The functions for updating the levels are in the form required for emulation by numerical methods: levels depart from their prior values by allowing their controlling rates’ influence to persist over a differential element of time D.
Higher-ordered delays are used as analogs to behaviors having more complexity than can be rendered by simple first-order or ‘exponential’ delays. The particulars behind such a statement can be as numerous as there are possible driving functions R. But differences in behavior between first order and higher ordered delays are best exposed for the case of an established steady-state, in which R = E, that is set on a course of dynamic adjustment by suddenly making the input rate R equal 0.
When this is done to the first-order delay, we observe the exponential pattern of decay introduced earlier. When this is done to a third-order delay, we observe the sigmoid pattern shown below.
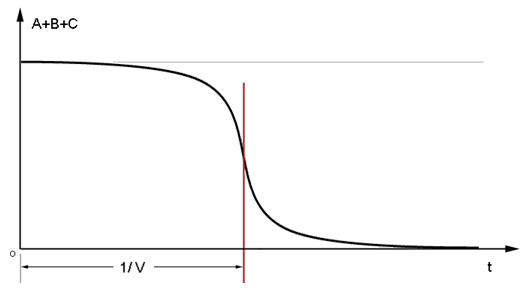
The sigmoid pattern of decay shows very little initial loss in the collected levels A + B + C. This is followed by a brief period in the vicinity of t = 1/V wherein the levels of A, B, and C deplete quite rapidly. The pattern is completed in a third phase characterized by levels that are now so low they have comparatively little force with which to propel their final exhaustion.
A sigmoid pattern of decay might be appropriate for mapping the useful life of a capital asset, such as a family automobile purchased with an intention to be used for, say, 1/V = 8 years. For much of the automobile’s useful life it functions as if new. As its age begins to approach the point for which its obsolescence has been designed, the automobile's functionality is only maintained by increasingly frequent and costly repairs. Finally, maintenance expenses are so high that the automobile is typically re-sold (i.e. re-valued) at a low enough price for it to be economically useful to its new owner.
A sigmoid pattern's exact shape is controlled by the number of levels in the higher-ordered delay by which the pattern is generated: the higher the delay’s order, the sharper the transition between initial and final states. Different orders of delay are therefore likely to be indicated for tracing out the useful economic lives of commodities composing an economic model. SFEcon's generic prototypes use third-order delays to emulate the processes by which economic goods exhaust themselves in producing the next generation of goods. But this is only a formality intended to hold place for a more incisive analysis.